JERARQUÍAS DE LAS GRAMÁTICAS (CHOMSKY)

ÁRBOLES

Diversos ejercicios sobre árboles generales y árboles binarios.
En breve...las soluciones!!

RETÍCULOS COMPLEMENTADO

RELACIÓN DE CONGRUENCIA

En esta entrada, veremos un ejemplo la relación de congruencia Zn.

Decimos que dos elementos a y b, pertencientes a Z, son congruentes módulo n si y solo si:

n|a-b

o

a-b=nk, siendo k un entero cualquiera

o

el resto de dividir a por n es igual al resto de dividir b por n.

 Por ser una relación de equivalencia, Zn produce una partición en Z, en clases de equivalencia.

Demostrar que Z5 es una partición de Z.

Veamos cómo son, explícitamente, las clases de congruencia módulo 5.

Comencemos por la clase de 0:

[0] = {xE Z/xR0} = { xE Z/x-0=5q  ^  qEZ}= {x E Z / x = 5q } 

[0]= {...,−20,−15,−10,−5,0,5,10,15,20,...};  

En las siguientes clases, expresamos lo mismo pero respetando la relación entre los elementos        

Escojamos un entero fuera de esta clase, digamos 1:

[1]={xE Z/xR1} = { xE Z/x-1=5q  ^  qEZ}= {x E Z / x = 5q+1^  qEZ}= {...,−19,−14, −9, −4,1,6,11,16,21,...};

Escojamos un entero fuera de las clases anteriores, por ejemplo 2:

[2]={xE Z/xR2} = { xE Z/x-2=5q  ^  qEZ}= {x E Z / x = 5q+2^  qEZ}={...,−18,−13, −8, −3,2,7,12,17,22,...};

Escojamos un entero fuera de las clases anteriores, por ejemplo 3:

[3]={xE Z/xR3} = { xE Z/x-3=5q  ^  qEZ}= {x E Z / x = 5q+3^  qEZ}={...,−17,−12, −7, −2,3,8,13,18,23,...};

Escojamos un entero fuera de las clases anteriores, digamos 4:

[4]= {xE Z/xR4} = { xE Z/x-4=5q  ^  qEZ}= {x E Z / x = 5q+4^  qEZ}={..., −16,−11, −6, −1,4,9,14,19,24,...};

¿Cumplen las condiciones para que constituyan una partición de Z?

1.   Cada clase de equivalencia es no vacía, ya que por lo menos contienen el elemento referente a ella.
2.  Estas clases son distintas dos a dos. ¿Por qué? Supongamos que un elemento x, un entero cualquiera,  pertenece  a la clase del  1 y también a la clase del 3, es decir suponemos que la intersección no es vacía. Si pertenece a la clase del 1: xR1 y si pertenece a la clase del 3: xR3, es decir que x= 5q₁+1 y x=5q₂+3 (aplicando la definición de la relación de congruencia módulo 5), que resulta absurdo, pues un mismo número al dividirlo por 5, tendrá siempre el mismo resto. Por lo tanto las clases son distintas dos a dos.
3. No es posible escoger un entero fuera de estas clases, dicho en otras palabras, si elegimos un entero cualquiera, estará en alguna de esas 5 clases. Es decir, que cualquier entero dividido por 5, nos dará como restos: 0, 1, 2,3y 4, que son precisamente las 5 clases halladas.

Se obtiene así una partición del conjunto Z de los enteros en cinco clases de congruencia módulo 5, y el conjunto cociente es

Z/(≡5) ={[0],[1],[2],[3],[4]}

.

ARITMÉTICA MODULAR

Para comenzar a comprender y manejar el concepto de la relación de congruencia.....unos ejercicios con números congruentes en diferentes módulos.
¡¡Intenten!!
Luego, subiré las respuestas.
Saludos
                 La Profe

RELACIONES BINARIAS

HOLA!!!
LES DEJO DOS APUNTES SOBRE EL TEMA...AL FINAL DE UNO DE ELLOS,HAY EJERCITACIÓN.
ESPERO LES QUEDE CLARO!!
UN ABRAZO!!!
LA PROFE

APUNTE SOBRE RELACIONES BINARIAS
OTRO APUNTE RELACIONES BINARIAS

Y UNA PRESENTACIÓN:

PREZZI SOBRE RELACIONES BINARIAS

LÓGICA MATEMÁTICA

En el siguiente link, encontrarán varios ejercicios de lógica resueltos:

                          EJERCICIOS DE LÓGICA

MODELOS DE FINALES

Para el 1° cuatrimestre del 2014:

Lo prometido es deuda....así que acá les dejo dos ejemplos de finales de Matemática Discreta.
El ejercicio sobre Grupos, solamente es para aquellos estudiantes que la cursaron antes del 2013.
Saludos!!!
Y Éxitos!!

                         La Profe

NÚMEROS COMBINATORIOS

Lógica proposicional

UNLaM

MATEMÁTICA DISCRETA

Hola!!
Les dejo dos links, uno de un apunte sobre lógica y el otro sobre razonamientos.
RAZONAMIENTOS:
https://www.dropbox.com/s/w0zb0qwqudgauov/RAZONAMIENTOS.pdf?dl=0

LÓGICA PROPOSICIONAL:
https://www.dropbox.com/s/c8433mksmwbky3i/L%C3%93GICA_.pdf?dl=0

SALUDOS!!!
                        La Profe

LÓGICA

ALGO MÁS SOBRE LÓGICA

Hola!!
Les dejo un pdf, con una presentación que hicimos con Marcela...
Es muy clara.
Saludos!!
                             La Profe


RESÚMEN DE LÓGICA PROPOSICIONAL

LÓGICA

UNLAM

Reglas de inferencia

Razonamientos lógicos

Navegando por la web, encontré el siguiente video sobre como resolver un razonamiento mediante reglas de inferencia..y un apunte sobre los mismos, con ejercicios resueltos....

Para leer el apunte o bajarlo a la pc, hagan click en el siguiente enlace:

Ejercicios Resueltos

Que tengan una semana excelente!!  

La Profe

LIBRO MATEMÁTICA DISCRETA

ROSEN: libro de cabecera de la cátedra Matemática Discreta


En este link podrán leer y bajar el libro de Rose, con el cual podrán hacer las actividades prácticas.

Matematicas_Discretas_-_Rosen.zip

Saludos!!
La Profe

LENGUAJES

Un breve resumen lleno de conceptos

Lenguajes from UNLAM

PARA MIS CHICOS DE ES 115 Y ESS 51

RESOLVAMOS ALGUNAS SITUACIONES…

1-      En el campamento hay un total de 60 carpas.

La mitad de las carpas son para 4 personas, una quinta parte de las carpas son para 2

personas y el resto de las carpas son para 6 personas.

Hoy todas las carpas están completas. ¿Cuántas personas hay en el campamento?

2-   Juan escribe dos números enteros distintos cuyo promedio es 68.

Los dos números son mayores que 50.

¿Cuál es el mayor número que puede escribir Juan?

 3

            3- En la figura:

A, D y E son cuadrados iguales;

B, C y F son rectángulos iguales.

El rectángulo formado por A y B tiene 60 cm de perímetro.

El rectángulo formado por B, C y F tiene 76 cm de perímetro.

¿Cuál es el perímetro de A?

¿Cuál es el perímetro de B?

¿Cuál es el perímetro de la figura?

.        4-  . En un triángulo ABC, el ángulo B  mide el doble que el ángulo A y el ángulo C  mide el  triple que el ángulo B  ¿Cuánto mide cada ángulo?

KAKUROS

KAKURO Y EL PENSAMIENTO ARITMÉTICO

 

Kakuro es una clase de enigma lógico-matemático. 

Los enigmas Kakuro son problemas de programación lineal, y se pueden resolver utilizando las técnicas de matriz matemática, aunque sean resueltos típicamente a mano.  Son de aparición regular en la mayoría de las publicaciones de matemáticas y de enigma lógico en varios países.

Dell Magazines propuso los nombres de Cross Sums (Sumas Cruzadas) y Cross Addition (Adición Cruzada), pero también el nombre japonés Kakuro (la abreviación japonesa de kasan kurosu: 加算クロス Adición+Cruz)

La popularidad de Kakuro en Japón es inmensa, sólo después del famoso Sudoku entre otras célebres ofertas de la famosa Nikoli, compañía editora japonesa que se especializa en juegos, y especialmente, en enigmas de lógica.

Reglas del juego

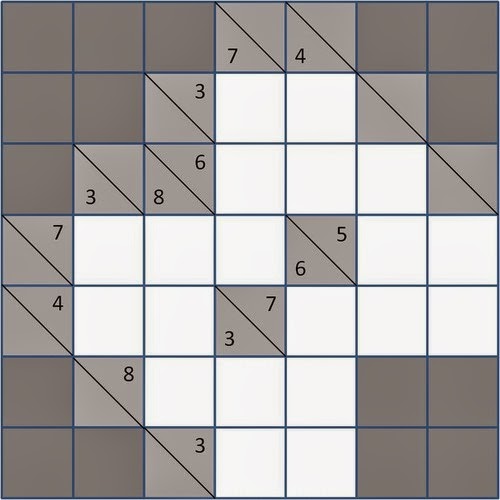
El objetivo consiste en rellenar las casillas vacías (color blanco) con los números de 1 al 9. Estas casillas se encuentran distribuidas en filas y columnas. Cada fila y columna contiene un número (en color blanco), llamado número clave. Este número indica la suma de la fila, si se encuentra a la izquierda de ésta, o la suma de la columna, si se encuentra arriba de ella.

Hay que rellenar las casillas vacías con números del 1 al 9, teniendo en cuenta que: cada fila o columna debe sumar lo indicado, y no se puede repetir un mismo número en una suma ya sea por fila o columna.

Ahora que conocemos algo más sobre el Kakuro...por que no resolvemos algunos??

Hasta pronto!

                                                              La Profe 

GRAFOS PLANOS

Grafos Planos

Un problema de aplicación de los grafos planos:

Cada una de las casas debe tener los tres servicios ( luz, agua y gas).

Ninguna de las conexiones puede cruzarse....¿ Cómo las realizan las distintas compañías?

¡Suerte!

TRABAJOS PRÁCTICOS MD

Buenas tardes!!

Como hoy les prometimos, les estoy subiendo los TP de las unidades 5,6 y 7, de Matemática Discreta.
Ahora podrán estudiar y practicar...como Uds querían!! 


Saludos!
                                                 La Profe

Trabajos Prácticos 5, 6 y 7.

COMBINATORIA

COMBINATORIA

¿CÓMO LAS DIFERENCIAMOS?

En este cuadro pueden ver bien las diferencias existentes...y por ende, cual aplicar, según el problema a resolver. Pero primordialmente, primero, deben interpretarlo bien!!

A pensar!!

                La Profe