JERARQUÍAS DE LAS GRAMÁTICAS (CHOMSKY)

ÁRBOLES

Diversos ejercicios sobre árboles generales y árboles binarios.
En breve...las soluciones!!

RETÍCULOS COMPLEMENTADO

RELACIÓN DE CONGRUENCIA

En esta entrada, veremos un ejemplo la relación de congruencia Zn.

Decimos que dos elementos a y b, pertencientes a Z, son congruentes módulo n si y solo si:

n|a-b

o

a-b=nk, siendo k un entero cualquiera

o

el resto de dividir a por n es igual al resto de dividir b por n.

 Por ser una relación de equivalencia, Zn produce una partición en Z, en clases de equivalencia.

Demostrar que Z5 es una partición de Z.

Veamos cómo son, explícitamente, las clases de congruencia módulo 5.

Comencemos por la clase de 0:

[0] = {xE Z/xR0} = { xE Z/x-0=5q  ^  qEZ}= {x E Z / x = 5q } 

[0]= {...,−20,−15,−10,−5,0,5,10,15,20,...};  

En las siguientes clases, expresamos lo mismo pero respetando la relación entre los elementos        

Escojamos un entero fuera de esta clase, digamos 1:

[1]={xE Z/xR1} = { xE Z/x-1=5q  ^  qEZ}= {x E Z / x = 5q+1^  qEZ}= {...,−19,−14, −9, −4,1,6,11,16,21,...};

Escojamos un entero fuera de las clases anteriores, por ejemplo 2:

[2]={xE Z/xR2} = { xE Z/x-2=5q  ^  qEZ}= {x E Z / x = 5q+2^  qEZ}={...,−18,−13, −8, −3,2,7,12,17,22,...};

Escojamos un entero fuera de las clases anteriores, por ejemplo 3:

[3]={xE Z/xR3} = { xE Z/x-3=5q  ^  qEZ}= {x E Z / x = 5q+3^  qEZ}={...,−17,−12, −7, −2,3,8,13,18,23,...};

Escojamos un entero fuera de las clases anteriores, digamos 4:

[4]= {xE Z/xR4} = { xE Z/x-4=5q  ^  qEZ}= {x E Z / x = 5q+4^  qEZ}={..., −16,−11, −6, −1,4,9,14,19,24,...};

¿Cumplen las condiciones para que constituyan una partición de Z?

1.   Cada clase de equivalencia es no vacía, ya que por lo menos contienen el elemento referente a ella.
2.  Estas clases son distintas dos a dos. ¿Por qué? Supongamos que un elemento x, un entero cualquiera,  pertenece  a la clase del  1 y también a la clase del 3, es decir suponemos que la intersección no es vacía. Si pertenece a la clase del 1: xR1 y si pertenece a la clase del 3: xR3, es decir que x= 5q₁+1 y x=5q₂+3 (aplicando la definición de la relación de congruencia módulo 5), que resulta absurdo, pues un mismo número al dividirlo por 5, tendrá siempre el mismo resto. Por lo tanto las clases son distintas dos a dos.
3. No es posible escoger un entero fuera de estas clases, dicho en otras palabras, si elegimos un entero cualquiera, estará en alguna de esas 5 clases. Es decir, que cualquier entero dividido por 5, nos dará como restos: 0, 1, 2,3y 4, que son precisamente las 5 clases halladas.

Se obtiene así una partición del conjunto Z de los enteros en cinco clases de congruencia módulo 5, y el conjunto cociente es

Z/(≡5) ={[0],[1],[2],[3],[4]}

.

ARITMÉTICA MODULAR

Para comenzar a comprender y manejar el concepto de la relación de congruencia.....unos ejercicios con números congruentes en diferentes módulos.
¡¡Intenten!!
Luego, subiré las respuestas.
Saludos
                 La Profe

RELACIONES BINARIAS

HOLA!!!
LES DEJO DOS APUNTES SOBRE EL TEMA...AL FINAL DE UNO DE ELLOS,HAY EJERCITACIÓN.
ESPERO LES QUEDE CLARO!!
UN ABRAZO!!!
LA PROFE

APUNTE SOBRE RELACIONES BINARIAS
OTRO APUNTE RELACIONES BINARIAS

Y UNA PRESENTACIÓN:

PREZZI SOBRE RELACIONES BINARIAS

LÓGICA MATEMÁTICA

En el siguiente link, encontrarán varios ejercicios de lógica resueltos:

                          EJERCICIOS DE LÓGICA

MODELOS DE FINALES

Para el 1° cuatrimestre del 2014:

Lo prometido es deuda....así que acá les dejo dos ejemplos de finales de Matemática Discreta.
El ejercicio sobre Grupos, solamente es para aquellos estudiantes que la cursaron antes del 2013.
Saludos!!!
Y Éxitos!!

                         La Profe

NÚMEROS COMBINATORIOS

Lógica proposicional

UNLaM

MATEMÁTICA DISCRETA

Hola!!
Les dejo dos links, uno de un apunte sobre lógica y el otro sobre razonamientos.
RAZONAMIENTOS:
https://www.dropbox.com/s/w0zb0qwqudgauov/RAZONAMIENTOS.pdf?dl=0

LÓGICA PROPOSICIONAL:
https://www.dropbox.com/s/c8433mksmwbky3i/L%C3%93GICA_.pdf?dl=0

SALUDOS!!!
                        La Profe

LÓGICA

ALGO MÁS SOBRE LÓGICA

Hola!!
Les dejo un pdf, con una presentación que hicimos con Marcela...
Es muy clara.
Saludos!!
                             La Profe


RESÚMEN DE LÓGICA PROPOSICIONAL

LÓGICA

UNLAM

Reglas de inferencia

Razonamientos lógicos

Navegando por la web, encontré el siguiente video sobre como resolver un razonamiento mediante reglas de inferencia..y un apunte sobre los mismos, con ejercicios resueltos....

Para leer el apunte o bajarlo a la pc, hagan click en el siguiente enlace:

Ejercicios Resueltos

Que tengan una semana excelente!!  

La Profe

LIBRO MATEMÁTICA DISCRETA

ROSEN: libro de cabecera de la cátedra Matemática Discreta


En este link podrán leer y bajar el libro de Rose, con el cual podrán hacer las actividades prácticas.

Matematicas_Discretas_-_Rosen.zip

Saludos!!
La Profe

LENGUAJES

Un breve resumen lleno de conceptos

Lenguajes from UNLAM

PARA MIS CHICOS DE ES 115 Y ESS 51

RESOLVAMOS ALGUNAS SITUACIONES…

1-      En el campamento hay un total de 60 carpas.

La mitad de las carpas son para 4 personas, una quinta parte de las carpas son para 2

personas y el resto de las carpas son para 6 personas.

Hoy todas las carpas están completas. ¿Cuántas personas hay en el campamento?

2-   Juan escribe dos números enteros distintos cuyo promedio es 68.

Los dos números son mayores que 50.

¿Cuál es el mayor número que puede escribir Juan?

 3

            3- En la figura:

A, D y E son cuadrados iguales;

B, C y F son rectángulos iguales.

El rectángulo formado por A y B tiene 60 cm de perímetro.

El rectángulo formado por B, C y F tiene 76 cm de perímetro.

¿Cuál es el perímetro de A?

¿Cuál es el perímetro de B?

¿Cuál es el perímetro de la figura?

.        4-  . En un triángulo ABC, el ángulo B  mide el doble que el ángulo A y el ángulo C  mide el  triple que el ángulo B  ¿Cuánto mide cada ángulo?

KAKUROS

KAKURO Y EL PENSAMIENTO ARITMÉTICO

 

Kakuro es una clase de enigma lógico-matemático. 

Los enigmas Kakuro son problemas de programación lineal, y se pueden resolver utilizando las técnicas de matriz matemática, aunque sean resueltos típicamente a mano.  Son de aparición regular en la mayoría de las publicaciones de matemáticas y de enigma lógico en varios países.

Dell Magazines propuso los nombres de Cross Sums (Sumas Cruzadas) y Cross Addition (Adición Cruzada), pero también el nombre japonés Kakuro (la abreviación japonesa de kasan kurosu: 加算クロス Adición+Cruz)

La popularidad de Kakuro en Japón es inmensa, sólo después del famoso Sudoku entre otras célebres ofertas de la famosa Nikoli, compañía editora japonesa que se especializa en juegos, y especialmente, en enigmas de lógica.

Reglas del juego

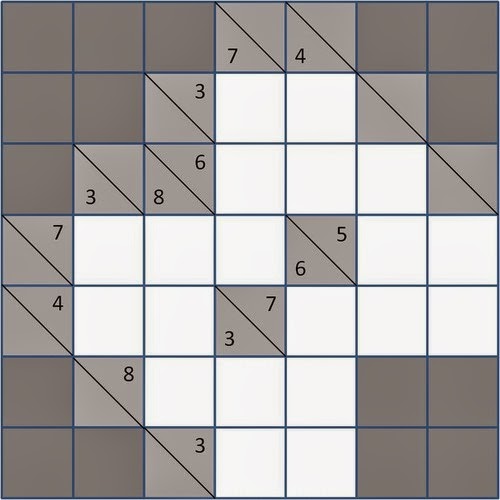
El objetivo consiste en rellenar las casillas vacías (color blanco) con los números de 1 al 9. Estas casillas se encuentran distribuidas en filas y columnas. Cada fila y columna contiene un número (en color blanco), llamado número clave. Este número indica la suma de la fila, si se encuentra a la izquierda de ésta, o la suma de la columna, si se encuentra arriba de ella.

Hay que rellenar las casillas vacías con números del 1 al 9, teniendo en cuenta que: cada fila o columna debe sumar lo indicado, y no se puede repetir un mismo número en una suma ya sea por fila o columna.

Ahora que conocemos algo más sobre el Kakuro...por que no resolvemos algunos??

Hasta pronto!

                                                              La Profe 

GRAFOS PLANOS

Grafos Planos

Un problema de aplicación de los grafos planos:

Cada una de las casas debe tener los tres servicios ( luz, agua y gas).

Ninguna de las conexiones puede cruzarse....¿ Cómo las realizan las distintas compañías?

¡Suerte!

TRABAJOS PRÁCTICOS MD

Buenas tardes!!

Como hoy les prometimos, les estoy subiendo los TP de las unidades 5,6 y 7, de Matemática Discreta.
Ahora podrán estudiar y practicar...como Uds querían!! 


Saludos!
                                                 La Profe

Trabajos Prácticos 5, 6 y 7.

COMBINATORIA

COMBINATORIA

¿CÓMO LAS DIFERENCIAMOS?

En este cuadro pueden ver bien las diferencias existentes...y por ende, cual aplicar, según el problema a resolver. Pero primordialmente, primero, deben interpretarlo bien!!

A pensar!!

                La Profe

EJERCICIOS RESUELTOS DE COMBINATORIA

 UNLAM

COMBINATORIA..

En este link...más de combinatoria resueltos!!!

COMBINATORIA

Excelente finde largo!!

Besos...

            Tere

COMBINATORIA

PROBLEMAS DE COMBINATORIA RESUELTOS.

Acá les dejo unos problemas que encontré navegando, buscando para uds!!!
Hay algunos con repetición...esos no van...pero si tienen ganas...pueden leerlos!!

Permutación

1) Se tienen 3 libros: uno de aritmética (A), uno de biología(B) y otro de cálculo(C), y se quiere ver de cuántas maneras se pueden ordenar en un estante.

En principio se puede elegir cualquiera de los 3 para colocar en primer lugar:

1a	2a	3a
A
B
C

  Una vez elegido uno de ellos, para ocupar el primer lugar, quedan 2 posibles para ubicar

Se ve entonces que hasta ahora hay 3.2 maneras distintas de ordenar los  libros. Pero una vez dispuestos las 2 primeros queda unívocamente determinado cuál debe ser el tercero.

O sea que el número total de maneras posibles de ordenar los 3 libros se puede calcular como: 3.2.1 = 6

Variación

2) Se tienen 7 libros y solo 3 espacios en una biblioteca, y se quiere calcular de cuántas maneras se pueden colocar 3 libros elegidos; entre los siete dados, suponiendo que no existan razones para preferir alguno.

En un principio se puede elegir cualquiera de los 7 libros para ubicarlo en

Primer lugar Después quedan 6 libros posibles para colocar en el segundo lugar y por último solo 5 libros para el tercer lugar.

Por lo tanto las distintas maneras en que se pueden llenar los 3 huecos de la

biblioteca es: 7.6.5 = 210

Si se tienen n libros y tres lugares es: n.(n - 1).(n - 2)

En general para n libros y k lugares resulta:

n. (n-1). (n-2). ..... .[n- (k-1)]

Con la fórmula: V_n,k = n!/(n-k)! _® V_7,3=7!/(7-3)!=7.6.5.4!/4!=7.6.5

PERMUTACIONES CON REPETICIÓN

3) ¿Cuántas permutaciones pueden formarse con las letras de la palabra BONDAD?

Hay 6!/2!

Si se escribe en lugar de BONDAD: BONDAD’

Todas las letras son distintas, luego hay 6! permutaciones, pero cada par de

permutaciones:

- - - D - D’

- - - D’- D

Coinciden, por lo tanto se tiene que dividir por 2 el número total de permutaciones

4) ¿De cuántas maneras se pueden ordenar las letras de la palabra AMASAS?

Si a la letras que se repiten se les coloca un subíndice se tiene

A ₁M A ₂ S ₁ A ₃ S₂ y el número de permutaciones posibles es P₆ = 6!

Que ocurre si sólo se cambian de posición las letras A?

A ₁M A ₂ S ₁ A ₃ S₂ A ₂M A ₃ S ₁ A ₂ S₂

A ₁M A ₃ S ₁ A ₂ S₂ A ₃M A ₁S ₁ A ₂ S₂

A ₂M A ₁ S ₁ A ₃ S₂ A ₃M A ₂ S ₁ A ₁ S₂

Se obtienen tantas maneras distintas de ordenar como permutaciones de 3

elementos (las 3 "A"), cuyo número es P₃ = 3!

De manera similar si sólo se modifica la posición de la letra "S" se obtienenP₂ = 2! maneras de ordenar diferentes.

Pero en cualquiera de los dos casos, siempre se sigue leyendo la misma palabra, es decir, que si se borran los subíndices, no se distingue diferencia alguna.

Se puede encontrar el número de permutaciones –P₆ distinguibles o no – haciendo el producto de las distinguibles – que se indican ₆ P _2,3 – por las no distinguibles P₂ y P₃ .

P₆ = ₆ P_2,3 . P₂. P₃

De esta manera se puede encontrar el número de permutaciones distinguibles:

P₆ /  P₂. P₃

Combinación

5) Un hospital cuenta con 21 cirujanos con los cuales hay que formar ternas para realizar guardias. ¿Cuántas ternas se podrán formar?

Se trata de formar todas las ternas posibles, sin repetir elementos en cada una, y sin importar el orden de los elementos.

Si quisiéramos formar todas las ternas posibles, sin repetición de elementos en cada una, para elegir el primer elemento hay 21 posibilidades, para el segundo quedan 20 posibilidades, y para el tercero 19 posibilidades, por lo tanto el número de ternas posibles está dado por: 21* 20*19 = 7980

Pero en este caso cada terna aparece repetida en distinto orden, por ejemplo tendremos: ABC, ACB, BAC, CAB y CBA. Son seis ternas con los mismos elementos, que está dado por el factorial de 3.

Por lo tanto el total de ternas obtenido 7980, hay que dividirlo por 6

7980/6 = 1330

Se pueden organizar las guardias de 1330 maneras diferentes

Este es un problema de combinación. Si llamamos m al número de elementos del conjunto y n al número que integrará cada uno de los conjuntos que debemos formar, de modo que ls elementos de cada uno sean diferentes y no importa el orden, se tiene la fórmula:

C_{m,n =} m!/ (n!. (m-n)!)

Combinaciones con repetición

6)¿De cuántas maneras pueden entrar cuatro alumnos en tres aulas, si no se hace distinción de personas?

Si tomamos, por ejemplo que entran dos personas en el aula 1, una en el aula 2 y otra en el aula 3

Que escribimos: 1123

Pero también se puede dar la siguiente situación

Es decir 3121

Otra situación

O sea 3211

Al no haber distinción estas distribuciones de cuatro alumnos en tres aulas son la misma.

Otra distribución distinta es, por ejemplo 1113, que significa: tres alumnos entraron en el aula 1 y el cuarto en el aula 3.

De modo que las distribuciones posibles de 4 personas en tres aulas, son

C’_3,4 = C_3+4-1,4 = C_6,4 = 6 . 5. 4. 3/(4. 3. 2. 1) = 15

7. Una comida gratis

Diez jóvenes decidieron celebrar la terminación de sus estudios en la escuela secundaria con un almuerzo en un restaurante. Una vez reunidos, se entabló entre ellos una discusión sobre el orden en que habían de sentarse a la mesa. Unos propusieron que la colocación fuera por orden alfabético; otros, con arreglo a la edad; otros, por los resultados de los exámenes; otros, por la estatura, etc. La discusión se prolongaba, la sopa se enfrió y nadie se sentaba a la mesa. Los reconcilió el camarero, dirigiéndoles las siguientes palabras:

• Jóvenes amigos, dejen de discutir. Siéntense a la mesa en cualquier orden y escúchenme

Todos se sentaron sin seguir un orden determinado. El camarero continuó:

• Que uno cualquiera anote el orden en que están sentados ahora. Mañana vienen a comer y se sientan en otro orden. Pasado mañana vienen de nuevo a comer y se sientan en orden distinto, y así sucesivamente hasta que hayan probado todas las combinaciones posibles. Cuando llegue el día en que ustedes tengan que sentarse de nuevo en la misma forma que ahora, les prometo solemnemente, que en lo sucesivo les convidaré a comer gratis diariamente, sirviéndoles los platos más exquisitos y escogidos.

La proposición agradó a todos y fue aceptada. Acordaron reunirse cada día en aquel restaurante y probar todos los modos distintos, posibles, de colocación alrededor de la mesa, con objeto de disfrutar cuanto antes de las comidas gratuitas.

Sin embargo no lograron llegar hasta ese día. Y no porque el camarero no cumpliera su palabra sino porque el número total de combinaciones diferentes alrededor de la mesa es extraordinariamente grande. Estas son exactamente 3.628.800. Es fácil calcular, que este número de días son casi 10.000 años.

Posiblemente a ustedes les parecerá increíble que 10 personas puedan colocarse en un número tan elevado de posiciones diferentes. Comprobemos el cálculo.

Ante todo, hay que aprender a determinar el número de combinaciones distintas, posibles. Para mayor sencillez empecemos calculando un número pequeño de objetos, por ejemplo, tres. Llamémosles A, B y C.

Deseamos saber de cuantos modos diferentes pueden disponerse, cambiando mutuamente su posición. Hagamos el siguiente razonamiento. Si se separa de momento el objeto C, los dos restantes, A y B, pueden colocarse solamente en dos formas.

Ahora agreguemos el objeto C a cada una de las parejas obtenidas. Podemos realizar esta operación tres veces:

1. colocar C detrás de la pareja,
2. colocar C delante de la pareja,
3. colocar C entre los dos objetos de la pareja.

Es evidente que no son posibles otras posiciones distintas para el objeto C, a excepción de las tres mencionadas. Como tenemos dos parejas, AB y BA, el número total de formas posibles de colocación de los tres objetos será: 2 x 3 = 6.

Hagamos el cálculo para cuatro objetos.

Tenemos cuatro objetos A, B, C y D, y separemos de momento uno de ellos, por ejemplo, el objeto D. Efectuemos con los otros tres todos los cambios posibles de posición. Ya sabemos que para tres, el número de cambios posibles es 6. ¿En cuántas formas diferentes podemos disponer el cuarto objeto en cada una de las 6 posiciones que resultan con tres objetos? Evidentemente, serán cuatro. Podemos:

1. colocar D detrás del trío,
2. colocar D delante del trío,
3. colocar D entre el 1º y de 2º objetos,
4. colocar D entre el 2º y 3º.

Obtenemos en total: 6 x 4 = 24 posiciones, pero teniendo en cuenta que 6 = 2 x 3 y que 2 = 1 x 2, entonces podemos calcular el número de cambios posibles de posición haciendo la siguiente multiplicación: 1 x 2 x 3 x 4 = 24.

Razonando de idéntica manera, cuando haya 5 objetos, hallaremos que el número de formas distintas de colocación será igual a: 1 x 2 x 3 x 4 x 5 = 120.

Para 6 objetos será: 1 x 2 x 3 x 4 x 5 x 6 = 720 y así sucesivamente.

Volvamos de nuevo al caso antes citado de los 10 comensales. Sabremos el número de posiciones que pueden adoptar las 10 personas alrededor de la mesa, si nos tomamos el trabajo de calcular el producto siguiente: 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10.

Resultará el número indicado anteriormente: 3.628.800.

El cálculo sería más complicado, si de los 10 comensales, 5 fueran muchachas y desearan sentarse a la mesa alternando con los muchachos. A pesar de que el número posible de combinaciones se reduciría en este caso considerablemente, el cálculo sería más complejo.

Supongamos que se sienta a la mesa, indiferentemente del sitio que elija, uno de los jóvenes. Los otros cuatro pueden sentarse, dejando vacías para las muchachas las sillas intermedias, adoptando 1 x 2 x 3 x 4 = 24 formas diferentes. Como en total hay 10 sillas, el primer joven puede ocupar 10 sitios distintos. Esto significa que el número total de combinaciones posibles para los muchachos es de 10 x 24 = 240.

¿En cuántas formas diferentes pueden sentarse en las sillas vacías, situadas entre los jóvenes las 5 muchachas? Evidentemente serán 1 x 2 x 3 x 4 x 5 = 120. Combinando cada una de las 240 posiciones de los muchachos, con cada una de las 120 que pueden adoptar las muchachas, obtendremos el número total de combinaciones posibles, o sea, 240 x 120 = 28.800

Este número, como vemos, es muchas veces inferior al que hemos citado antes y se necesitaría un total de 79 años. Los jóvenes clientes del restaurante, que vivieran hasta la edad de cien años, podrían asistir a una comida, servida gratis, si no por el propio camarero, al menos por uno de sus descendientes.

Sabiendo calcular el número de permutaciones posibles, podemos determinar el número de combinaciones realizables con las cifras del "juego del 15". Con otras palabras, podemos calcular el número total de ejercicios que es posible efectuar con ese juego. Se comprende fácilmente, que el cálculo se reduce a hallar el número de combinaciones posibles a base de 15 objetos. Sabemos, según hemos visto, que para ello es preciso multiplicar sucesivamente: 1 x 2 x 3 x 4 x … x 14 x 15.

Como resultado se obtiene: 1.307.674.365.000, o sea, más de un billón.

La mitad de ese enorme número de ejercicios son insolubles, o sea que en este juego, más de 600.000 millones de combinaciones no tienen solución. Por ello se comprende, en parte, la fiebre de apasionamiento por el "juego del 15", que embargó a las gentes, que no sospechaban la existencia de ese inmenso número de casos insolubles.

Si fuera posible colocar cada segundo las cifras en una nueva posición, para realizar todas las combinaciones posibles, habría que trabajar incesantemente día y noche más de 40.000 años.

Como fin de nuestra charla sobre el número de combinaciones posibles, resolvamos el siguiente problema relacionado con la vida escolar.

Hay en clase 25 alumnos. ¿En cuántas formas diferentes pueden sentarse en los pupitres?

Para los que han asimilado lo expuesto anteriormente, la solución es muy sencilla: basta multiplicar sucesivamente los 25 números siguientes: 1 x 2 x 3 x 4 x 5 x 6 x … x 23 x 24 x 25.

En matemáticas existen diversos métodos de simplificación de los cálculos, pero para facilitar operaciones como la que acabamos de mencionar, no los hay. El único procedimiento para efectuar exactamente esta operación consiste en multiplicar con paciencia todos esos números. Sólo puede reducirse algo de tiempo requerido para efectuar esa multiplicación, eligiendo una agrupación acertada de los mismos. El resultado que se obtiene es un número enorme compuesto de 26 cifras, cuya magnitud es incapaz de representársela nuestra imaginación.

He aquí el número: 15.511.210.043.330.985.984.000.000