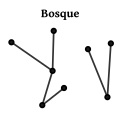PROFE TERE FERNÁNDEZ Y LAS MATES: julio 2012

UNLaM

Grafos...algunos conceptos.

Un grafo es una terna G=(V,A, f), donde V es un conjunto finito no vacío (a cuyos elementos llamaremos vértices) y A es una familia finita de pares no ordenados de vértices de V (a cuyos elementos llamaremos aristas o arcos) y f la función de incidencia entre vértices y aristas.

Un grafo simple : el que no tiene aristas paralelas ni lazos o bucles.

Dos vértices son adyacentes si son extremos de una misma arista.

Dos aristas son adyacentes si tienen un extremo común.

Un vértice y una arista son incidentes si el vértice es extremo de la arista.

Un vértice es aislado si no tiene otros vértices adyacentes.

Un grafo completo es un grafo simple en el que todo par de vértices está unido por una arista. (Se representa con K_n al grafo completo de n vértices). La relación entre cantidad de vértices y cantidad de aristas es la siguiente: Si n es el cardinal de vértices y a el cardinal de aristas, se cumple lo siguiente:

a= n.(n-1)/2

Un grafo G se llama bipartido si existe una partición de V, V=X È Y, tal que cada arista de G une un vértice de X con otro de Y.

Se designa por K_r,s al grafo bipartido completo en el que hay una arista que conecta cada vértice de X con cada vértice de Y. En este grafo V= r+s y A= r.s (representando V a la cantidad de vértices y A la cantidad de aristas.)

Dos grafos simples G=(V,A) y G’=(V’,A’) son isomorfos si existe una biyección f: que conserva la adyacencia.. ( número de vértices y aristas coinciden, tienen los mismos recorridos, la misma adyacencia y vecindad, sus matrices de adyacencias, no son necesarimente iguales, pero el valor del determinante de cada una es igual).

GRADO

Se llama grado de un vértice v al número de aristas que lo tienen como extremo, (cada bucle se cuenta, por tanto, dos veces). Se designa por g(v)

Un grafo regular es un grafo simple cuyos vértices tienen todos el mismo grado.

$\sum_{v \in V} g(v) = 2|E|\,$

La relación entre los grados y el número de aristas en G .

Es decir, que siempre la suma de todos los grados de un grafo es un número par.

CAMINOS Y CONEXIÓN
Un camino es una sucesión de vértices tal que de cada uno de sus vértices existe una arista hacia el vértice siguiente.
La longitud de un camino es el número de aristas que usa dicho camino, contando aristas recorridas varias veces el mismo número de veces que las recorramos
Un camino simple es aquel en que todas las aristas del camino son diferentes.
Un Ciclo (o circuito) es un camino que empieza y acaba en el mismo vértice. Los ciclos de longitud 1 son los bucles.
Un ciclo simple es un ciclo que tiene como longitud al menos 3 y en el que el vértice del comienzo sólo aparece una vez más y como vértice final, y los demás sólo aparecen una vez.

Un grafo es conexo si para cada par de vértices u y v existe un camino de u a v. Si G es un grafo no conexo (o disconexo), cada uno de sus subgrafos conexos maximales se llama componente conexa de G.

Un vértice v se llama ISTMO de G si el grafo G-{v}no es conexo.

Conectividad: es el número de vértices que debemos sacar para que el graf deje de ser conexo.

Una arista a de un grafo G se llama PUENTE si G-{a} no es conexo.

Conjunto desconectante: es el conjunto de aristas que debemos sacar para que el grafo deje de ser conexo.

RECORRIDOS EN UN GRAFO
Un camino euleriano en un grafo es un camino que contiene a todas las aristas del grafo exactamente una vez. Este recorrido puede repetir vértices .Un grafo es euleriano si contiene un camino euleriano cerrado.
Teorema: Un grafo conexo G es euleriano Û Todos los vértices de G tienen grado par.
Consecuencia: Un grafo conexo G tiene un camino euleriano no cerrado Û G tiene, exactamente, dos vértices de grado impar.

$C=\{ 1,2,3,4,6,3,5,4,1\}\,$ es un ciclo euleriano,

Un camino hamiltoniano en un grafo es un camino que contiene a todos los vértices del grafo exactamente una vez (salvo v₀=v_n, si el camino es cerrado).Este recorrido puede repetir aristas, o no recorrerlas a todas. Un grafo hamiltoniano es aquel que contiene un ciclo hamiltoniano.
Propiedad: Un grafo bipartido G=(V_1 ÈV₂, A) con ½ V_1½ ¹ ½V_2½no es hamiltoniano.
Teorema: Sea G un grafo simple de n vértices. Si para todo par de vértices x e y no adyacentes se cumple que g(x)+g (y) ³ n , entonces G es hamiltoniano.
Teorema: Si G es un grafo hamiltoniano entonces, para todo SÌ V se cumple que el número de componentes conexas de G - S, es menor o igual que ½ S½ .
Todos los sólidos platónicos, (tetraedro, el cubo, el octaedro, el dodecaedro y el icosaedro.) considerados como grafos, son hamiltonianos.
Todos los grafos completos son hamiltonianos.
Un grafo con n vértices (n > 3) es hamiltoniano si cada vértice tiene grado mayor o igual a n/2.
Un grafo con n vértices (n > 3) es hamiltoniano si la suma de los grados de 2 vértices no adyacentes es mayor o igual que n.

CICLO HAMILTONIANO

ÁRBOLES

Un árbol es un grafo conexo y sin ciclos.
Propiedades
            1) Para todo par de vértices x e y existe un único camino de x a y.
            2) Todas las aristas de G son puentes.
            3) ½ A½ = n - 1. , siendo n el cardinal de Vértices.
            4) Todo árbol tiene al menos dos hojas (vértices de grado uno).
5) $\sum_{v \in V} g(v) = 2|E|\,$
Un bosque es un grafo acíclico. Si tiene k componentes conexas entonces el nº de aristas es n- k.

Un árbol generador de un grafo G, es un subgrafo que es árbol y contiene a todos los vértices del grafo.
Todo grafo conexo posee un árbol generador.
Un árbol con raíz es un árbol T con un vértice distinguido al que se denomina raíz. Este vértice se representa encima de los restantes, que se colocan por niveles según su distancia a la raíz. Nivel de la raíz: 0.
Se llama altura (o profundidad) de un árbol con raíz a la máxima distancia de un vértice a la raíz.Es decir es el último nivel.
Para cada vértice u, que no sea la raíz, se llama padre de u al único vértice adyacente a u que se encuentra en el camino de u a la raíz. Se llaman hijos de u a los restantes vértices adyacentes, (que se encuentran por debajo de u). Los vértices sin hijos son las hojas del árbol, y los vértices que no son hojas ni raíz se denominan vértices interiores.
Un árbol n-ario es un árbol con raíz en el que cada padre tiene, a lo sumo, n hijos.
Propiedades: 1) El número de hojas de un árbol m-ario es, a lo más, m^h.
2) La altura de un árbol m-ario de l hojas es, al menos, ë log _mlû
Árbol balanceado: las hojas se encuentran en el último nivel y/o en el anteúltimo.
Árbol n-ario regular: es un árbol con raíz en el que cada padre tiene exactamente n hijos.
Árbol n-ario regular pleno o completo: es un árbol donde cada padre tiene exactamente n hijos ( salvo las hojas) y todas las hojas se encuentran en el último nivel.
Árbol binario: todos los padres tienen dos hijos. Son los que se llaman también operacionales.

Recorridos: Podemos recorrerlos de tres formas: preorden, in orden o post orden.

A cada uno le corresponde la siguiente notación:

Preorden: Notación polaca: +3 4 = 3+4. Decimos al recorrerlo padre-hijo-hijo. Su recorrido es: Raíz- Subárbol izquierdo- Saubárbol derecho, todo en preorden.

In orden: Notación usual 3+4= 3+4. Lo recorremos así hijo-padre-hijo. Recorrido es : Subárbol izquierdo- Raíz-Subárbol derecho.

Este tipo de notación no nos da la caracterización de un árbol únicamente, por lo cual no nos sirve para recorrerlos.

Postorden: Notación polaca inversa 3 4 + = 3+4. Decimos al recorrerlo -hijo-hijo-padre Su recorrido es: Subárbol izquierdo- Subárbol derecho- raíz todo en postorden.

Ejemplos: